Современные формы обучения, инновации в преподавании, введение новых технологий диктуют учителю необходимость постигать секреты мастерства, а значит, и совершенствовать методы обучения и воспитания учащихся.

Исследования психологов и педагогов, опыт коллег показывают: чтобы научить детей самостоятельно учиться и проявлять творчество необходимо применение деятельностного подхода в обучении. Для этого учащихся нужно замотивировать и обучить их приемам и способам учебной деятельности, которые помогут сформировать необходимые знания, умения и навыки.

Курс школьной математики имеет достаточно широкие возможности для применения различных приемов, методов и технологий. В последние годы в содержание школьного курса естественным образом закладывается алгоритмическая линия. Так как применение алгоритмов является приоритетным в моей работе, то нужно отметить что, между понятиями “прием” и “алгоритм” существует много общего, ни и есть принципиальные отличия, а именно:

– прием – это рациональный способ работы, который состоит из отдельных действий, он может быть выражен в виде правил или инструкций, его можно перестроить и на его основе создать новый прием. Приемы деятельности допускают самостоятельный выбор учениками конкретных действий по решению учебных задач;
– алгоритм – это общепонятное и однозначное предписание, которое определяет последовательность действий, позволяющее достичь искомый результат. Алгоритм предполагает жесткое выполнение шагов, а прием дает общее направление деятельности по решению учебных задач, не регламентируя каждый шаг. Поэтому я в своей работе выделяю два подхода: 1) обучение алгоритмам; 2) формирование приемов решения задач. Школьные задачи делятся на: алгоритмические, полуалгоритмические, полуэвристические и эвристические. Каждый тип задачи предполагает свои схемы решения, подходы, применение логики и изобретательности.

На начальном этапе обучения математике применение алгоритмов способствует формированию и прочному усвоению навыков владения математическими методами. Также осуществляется подготовка к формированию первоначальных представлений о математическом моделировании. Уже в начальных классах прослеживается применение простейших алгоритмов выполнения арифметических операций, дети овладевают навыками выполнения последовательных действий. Решают задачи с составлением схем и кратких записей. Это можно рассматривать как пропедевтику операционного стиля мышления.

Следующий уровень алгоритмической культуры учащихся – введение понятия алгоритма и формирование его основных свойств. Это происходит в среднем звене школы. Именно в этот период необходимо сочетания алгоритма и образца ответа, что дает возможность ученику, верно, ответить на поставленный вопрос, сопроводив его правильной речью. У учителя появляется возможность предлагать задачи с элементами творчества. А материал, предлагаемый в наших школьных учебниках, является хорошей базой для обучения составлению простейших алгоритмов и дальнейшей их записи в разных формах. Мы применяем табличную, графическую (блок-схема), словесную и формульную форму записи алгоритмов.

В качестве примера, иллюстрирующего процесс алгоритмизации как средство обучения, можно указать на решение задач методом уравнений. Примером графического алгоритма является блок-схема для отыскания количества решений системы двух линейных уравнений с двумя неизвестными (см. Рисунок 1).

Отыскания числа решений системы двух линейных уравнений (блок-схема)

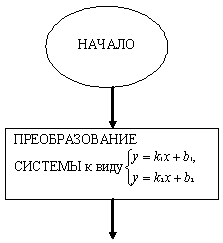
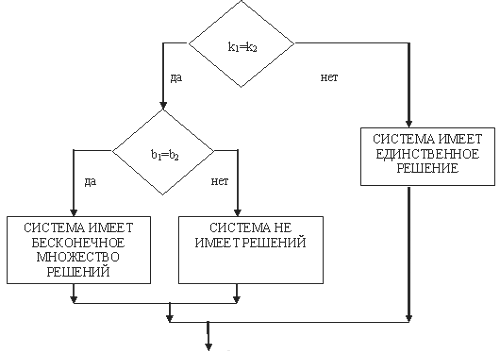
Рис. 1
Графические алгоритмы

Табличную форму алгоритма можно продемонстрировать на примере таблицы, составляемой для исследования функций и дальнейшего построения графиков (см. рис. 2).

Исследование функции и построение графика

Функция задана уравнением у = f(x). Исследовать функцию и построить ее график.

1. Таблица исследования функции

2. Построение графика

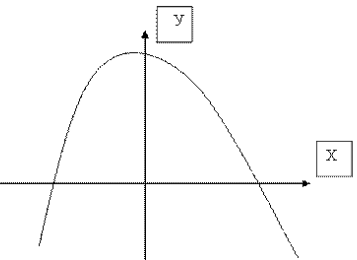
Рис. 2
Табличный алгоритм

Пример формульного способа – последовательность нахождения компонентов при составлении уравнения касательной к графику той или иной функции (см. рис. 3).

Уравнение касательной к графику функции

Рис. 3
Формульный способ

Словесный алгоритм используется практически во всех правилах выполнения действий, например, правило сложения чисел с разными знаками (см. рис. 4).

Алгоритм сложения чисел с разными знаками

Рис. 4
Словесный алгоритм

В старших классах работа становится разнообразней и содержательней, появляется возможность включать упражнения разного типа и уровня сложности, предполагающее, что приемы деятельности могут быть разной степени сложности и обобщенности. Они состоят из большого числа действий, выполнение которых приводит к применению алгоритмов на отдельных этапах работы.

Такой подход к преподаванию математики в основной школе определяет условия для формирования у учащихся навыков, позволяющих в старших классах успешно изучать базовый курс “Информатики и ИКТ”. Применение алгоритмов в старших классах, по мнению некоторых учителей, отбивает творческий подход к решению задач, но с другой стороны, твердое знание основных задач курса и умение их решать, является твердым фундаментом для активизации самостоятельной и творческой работы учащихся.